Hadoop MapReduce: Content Based Authorship Detection using TF/IDF Scores and Cosine Similarity
Introduction:
The goal is to build an authorship detection system that provides a ranked list of possible authors for a document whose authorship is unknown. The system uses N-gram analysis from this project. In particular, I used the word uni-grams from that project. Finding the attributes of literature content written by an author is important to detect unique writing style for that author. I built an attribute vector for each of the authors with the help of Term Frequency and Inverse Document Frequency (TF-IDF) analysis. Authorship is determined based on the similarity between the attribute vectors of the unseen document and the pre-computed attribute vectors of authors. TF-IDF is used to calculate the weights of each of the entities in the attribute vector.
Definitions:
Term Frequency:
Let's assume that we have a collection of documents written by M authors. This collection of documents may contain multiple books written by an author. Let’s define a set of documents written by same author as a sub-collection $j$. We define $f_{ij}$ to be the frequency (Number of occurrences) of term (word) $i$ in sub-collection $j$.
\begin{equation} TF_{ij} = 0.5 + {f_{ij} \over max_k f_{kj}} \label{eq:tf1} \end{equation}
We use the augmented $TF$ (represented by 0.5 added initially in term 1 and then multiplied in terms 2 of \eqref{eq:tf1}) to prevent a bias towards longer documents. Term 2 is the raw frequency divided by the maximum raw frequency of any term $k$ in the sub-collection $j$. Stop words (e.g., a, an, the, etc) were not eliminated from the corpus. The most frequent term in the sub-collection will have a augmented $TF$ value of 1.
Inverse Document Frequency:
Suppose that term $i$ appears in $n_i$ sub-collections within the corpus. For this assignment, we define the $IDF_i$, as: \begin{equation} IDF_i = log_{10} ({N \over n_i}) \label{eq:idf1} \end{equation} where, $N$ is the total number of sub-collections (same as the number of authors).
TF-IDF value:
The TF-IDF score is the product - $TF_{ij}$ $\times$ $IDF_i$. The terms with the highest TF-IDF score are considered the best words that characterize the sub-collection (document). They are the most important attributes in the sub-collection's attribute vector.
Cosine Distance between Attribute Vectors:
After calculating the TF, IDF, and TF-IDF scores for set of books written by the same author (sub-collection) in the corpus, we generate an Author Attribute Vector (AAV) as follows: Every author will have their own AAV representing their unique writing style with the help of TF-IDF score of words in the entire corpus. In order to find authorship of a unseen document, we compare the AAV of that document with AAVs of all the possible authors. Note that to compare an arbitrary AAV (from the document with unknown authorship) and existing AAVs, all of the AAVs must have the same dimension. For this comparison we calculate the Cosine Distance between two AAVs that gives a measure of similarity between the authors’ writing styles. Suppose that we have two authors with vectors, $AAV_1 = [x_1 , x_2 , ..., x_m]$ and $AAV_2 = [y_1 , y_2 , ..., y_m]$. The Cosine Similarity between them is defined as,
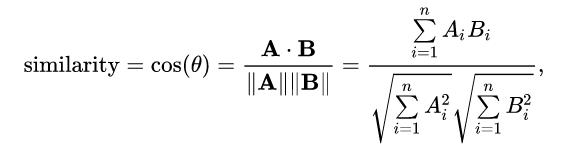
Where $AAV_1$ is represented by $A$ and $AAV_2$ by $B$. Using this formula, we will be able to create a ranked list of potential authors for a given document with unknown authorship. Logically, the author with highest cosine similarity with given document will be the most probable author of the document.
Dataset:
Read the dataset description from a previous post.
Methodology:
- Part 1: Calculate the TF, IDF, and TF-IDF values for all terms for all of the sub-collections in the corpus.
- Part 2: Create the AAVs (author attribute vectors) for every author.
- Part 3: Find cosine similarity between AAV of given document with unknown author and all the authors in the corpus.
Outputs:
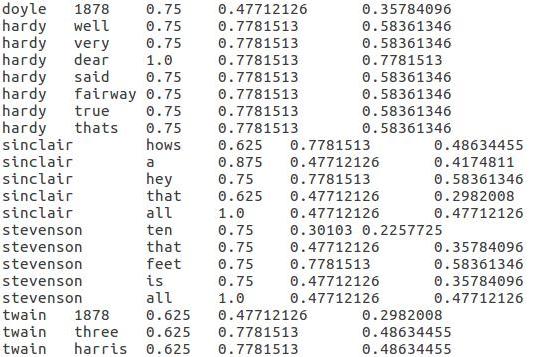
Originally, we used the complete dataset as described above in the dataset section to found AAVs for all the authors in that dataset and then calculated their cosine similarity metric with AAV of the given document with unknown author. But for the purpose of illustration I will use a very small toy dataset containing 12 lines that can be found here.The authorAttrVect_toy_dataset_illustration direcory contains a very small toy dataset fed as input to the system and the outputs at every map reduce step of authorAttrVect map-reduce program from the repo. The final output is mr4aav12.txt that contains TF-IDF scores in the final column. Here is a snippet from the output of map-reduce described programs above.
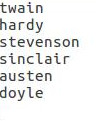
Finally, we provide a document with unknown authorship to the cosineSimilarity map-reduce program. It produces the list of potential that are could have written that document. Suppose we fed a document written twain as a document with unknown authorship. The cosineSimilarity program will produce a list of potential authors like this one:
Note: Some of the content for this post is taken from course material of CS435 (CSU) written by Prof. Sangmi Lee Pallickara and GTAs.