Smoothing .obj 3D models

Introduction:

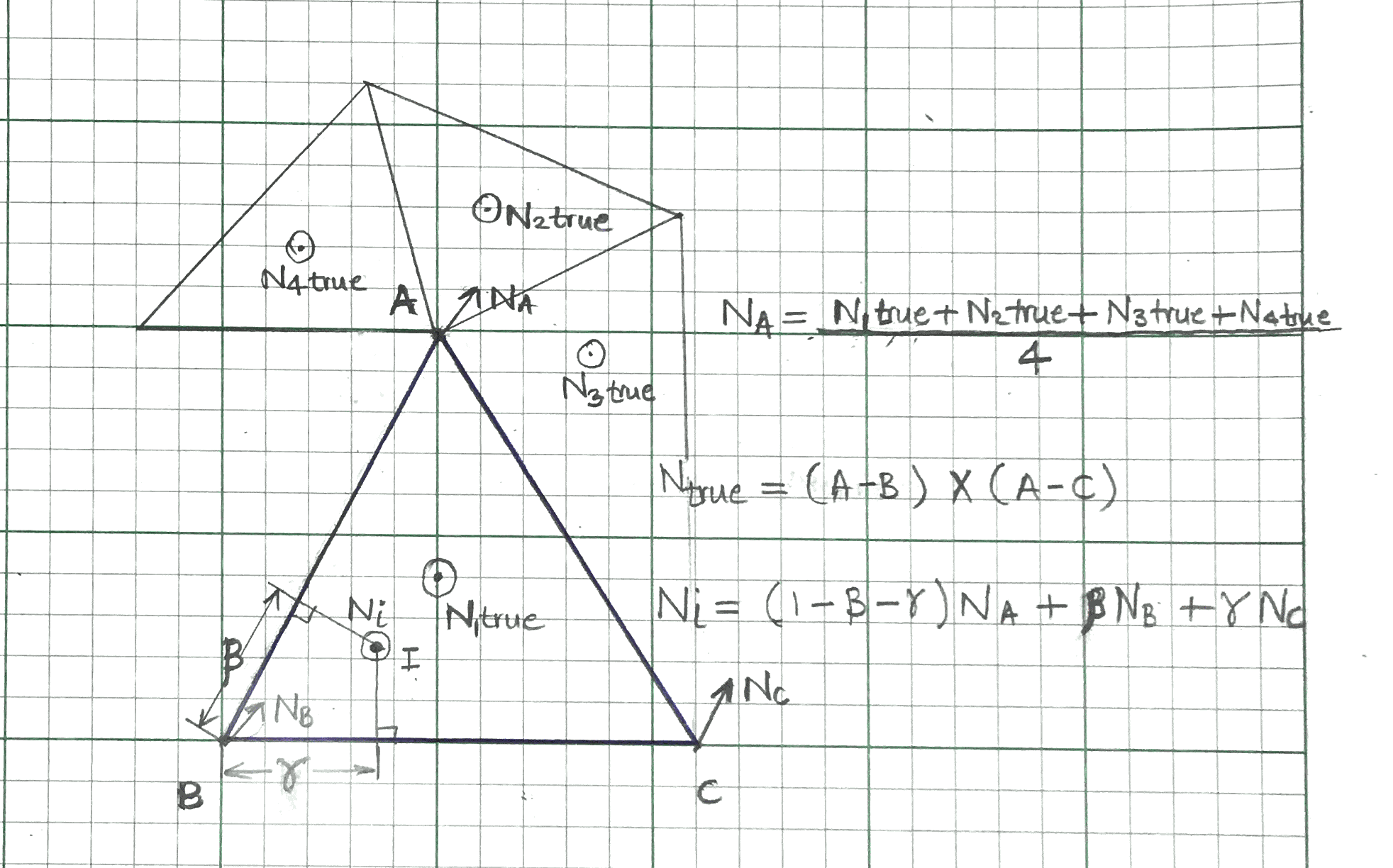
A .obj file is usually defined in terms of triangle that form the faces of a 3D object. They follow Wavefront .obj file format. Each face and vertex forming that face has a normal associated with it. The transition of these normals going from one face to the next adjacent face is not smooth. When you render a .obj file without smoothing these normals, you get a object that shows triangular artifacts as shown in the Figure 2a. With this approach, for every location on a specific triangular face, there is single normal associated with it. This normal ($N_{true}$) can either be read from the .obj file or can be calculated using cross product of the edge vectors of that triangle using the formula in \eqref{eq:nt1}.
\begin{equation} N_{true} = (A - B) \times (A - C) \label{eq:nt1} \end{equation}

However, it is possible to get a smooth rendering of a .obj file by smoothing out the transitions of normals going from one face to the adjacent faces. With this approach, the normal at a point on the triangular face is calculated dynamically depending on what point we want to render on our image plane. In this case, the normal at point $I$ on a triangular face is defined by \eqref{eq:ni1}
\begin{equation} N_{true} = (1 - \beta - \gamma)*N_{A} + \beta*N_{B} + \gamma*N_{C} \label{eq:ni1} \end{equation}
Here, $N_{A}$, $N_{B}$, and $N_{C}$ are the mean normals at vertex $A$, $B$, and $C$ respectively of the triangular face. The constants $\beta$ and $\gamma$ are the distances of point $I$ from vertex $A$ along the edges of the triangular face.

Now, the mean normal at any vertex, say vertex $A$, can be found using simply averaging the $N_{true}$ of all the triangular faces in that .obj file that share the vertex $A$ using \eqref{eq:av1}.
\begin{equation} N_{A} = mean(N1_{true}, N2_{true}, N3_{true}, N4_{true}, ....) \label{eq:av1} \end{equation}
You can find the mean normals for vertex $B$ and $C$ using similar logic.

However, there is one more check that ensures that we are not smoothing out the edges of sharp objects such as a cube. With cube, you should not find mean of two adjacent triangles belonging to adjacent square faces of the cube, because that will smooth out the edge of the cube that we do not intend to smooth. Similar goes with the corners of the cube or the pointy horn of the cow in Figure 3a which should not be smoothed. Therefore to avoid smoothing the sharp parts of the .obj file you should ensure that when finding the mean vertex normal (as in \eqref{eq:av1}), the normals that are being averaged are within some angle $\delta$ of the $N1_{true}$ of the face in consideration. Figure 3b shows smoothing with $\delta = 22^\text{o}$. For Figure, 4 and 5 the $\delta$ is gradually increased with $\delta$ equal to $30^\text{o}$, $45^\text{o}$, and $60^\text{o}$. As you can see, with higher $\delta$ threshold we get more smoothly rendered object.