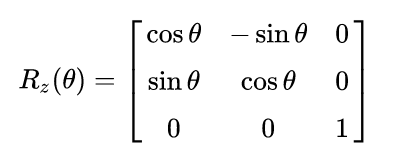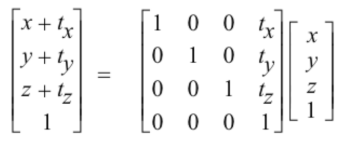Transforming 3D Graphics Objects Defined in Geometry Definition File Formats (.ply, .obj) using axis-angle rotation
Introduction:
In 3D graphics, people often use geometry definition file formats such as Wavefront .obj format or Polygonal File Format .ply to render objects in a scene. These formats store the object in that are defined in terms of polygons. These objects are stored in a 3D reference frame of its own. When you have to render multiple objects with their own frame of reference into one scene having a global (world) frame of reference, you need to transform individual objects into that world frame of reference.
Transformation of a 3D object from one frame of reference to another can be achieved by a series of transformations such as Rotation, Scale, and Translation. These transformations are applied to points in 3D that describe the vertices of our polygonal objects. We will go over individual transformation below.
You can read more about the internals of this project here.
Rotation (Axis-Angle-Rotation Technique):
Axis-angle rotation technique is a standard way to rotate about a specified axis wx wy wz by a specified angle theta in radians.
Axis-angle rotation can be divided into three steps as follows:
- Rotate data points to make axis-z the axis of rotation.
- Rotate data points about axis-z.
- Apply the inverse of the original rotation from step 1.
\begin{equation} P' = ({R_{w}^{-1} R_{Z_{Theta}} R_{w}}) \cdot {P} \label{eq:t1} \end{equation}
where, each $R$ matrix (from right to left) corresponds to one step from 3 steps described above. Here, we represent point $P_{A}$ in homogeneous coordinates format with $w = 1$.
Therefore, $P_{A} = [x, y, z, w]'$
Step 1 - $R_{w}$:
$R_{w}$ is defined as below:
Step 2 - $R_{Z_{Theta}}$:
$R_{Z_{Theta}}$ is a standard rotation matrix to rotate about axis-z. Now using Euler's Rotation Theorem,
Step 3 - $R_{w}^{-1}$:
Since $R_{w}$ is a rotation matrix with all its vectors being unit length, its inverse is its transpose matrix. Therefore, $R_{w}^{-1} = R_{w}^{'}$.
Scaling:
In order to scale the point $P_{A} = [x, y, z, 1]'$, by a scaling factor sx sy sz, following scaling equation is used,
Translation:
In order to translate the point $P_{A} = [x, y, z, 1]'$, by a translation factor tx ty tz, following translation equation is used,
Results:
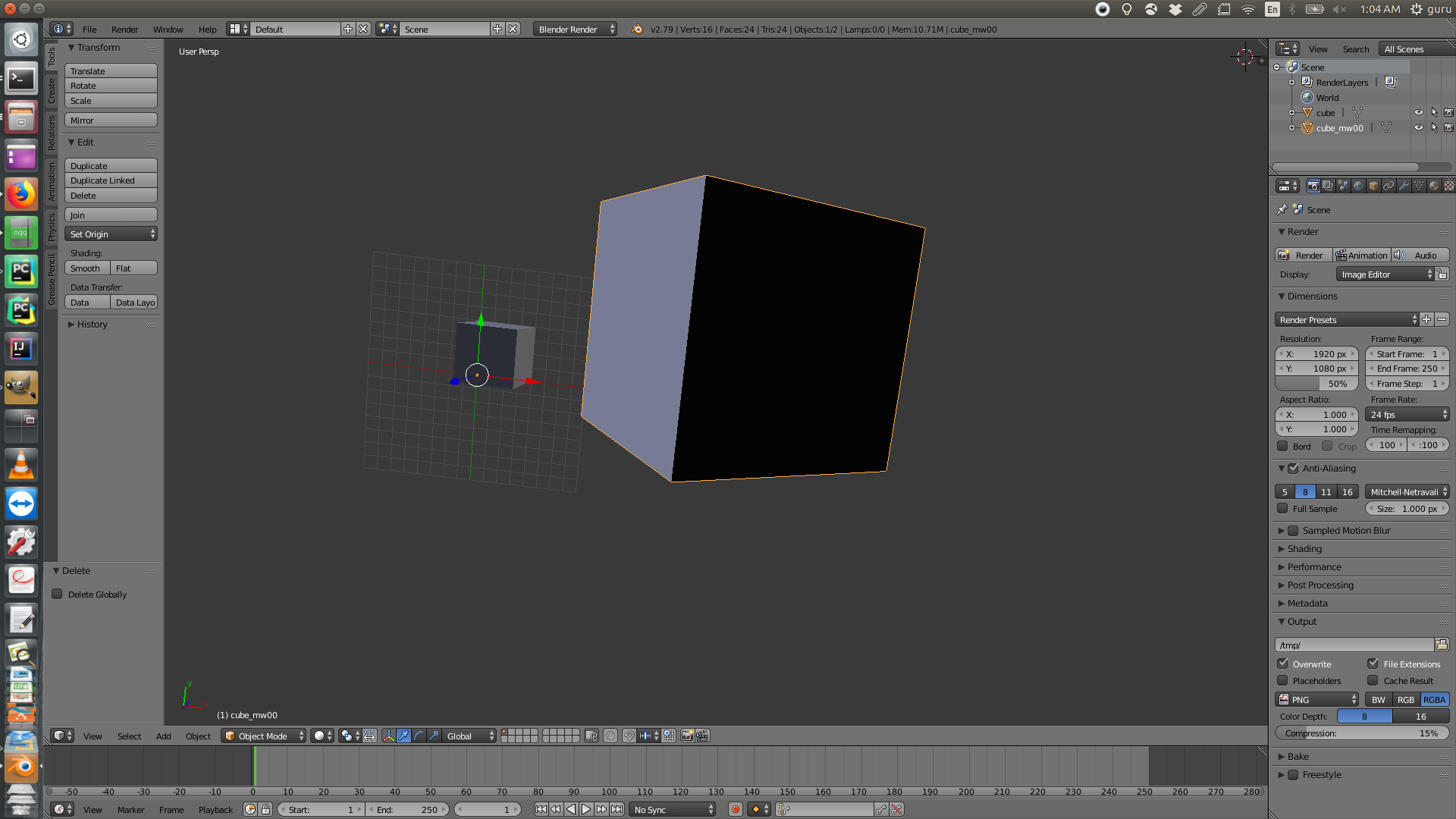
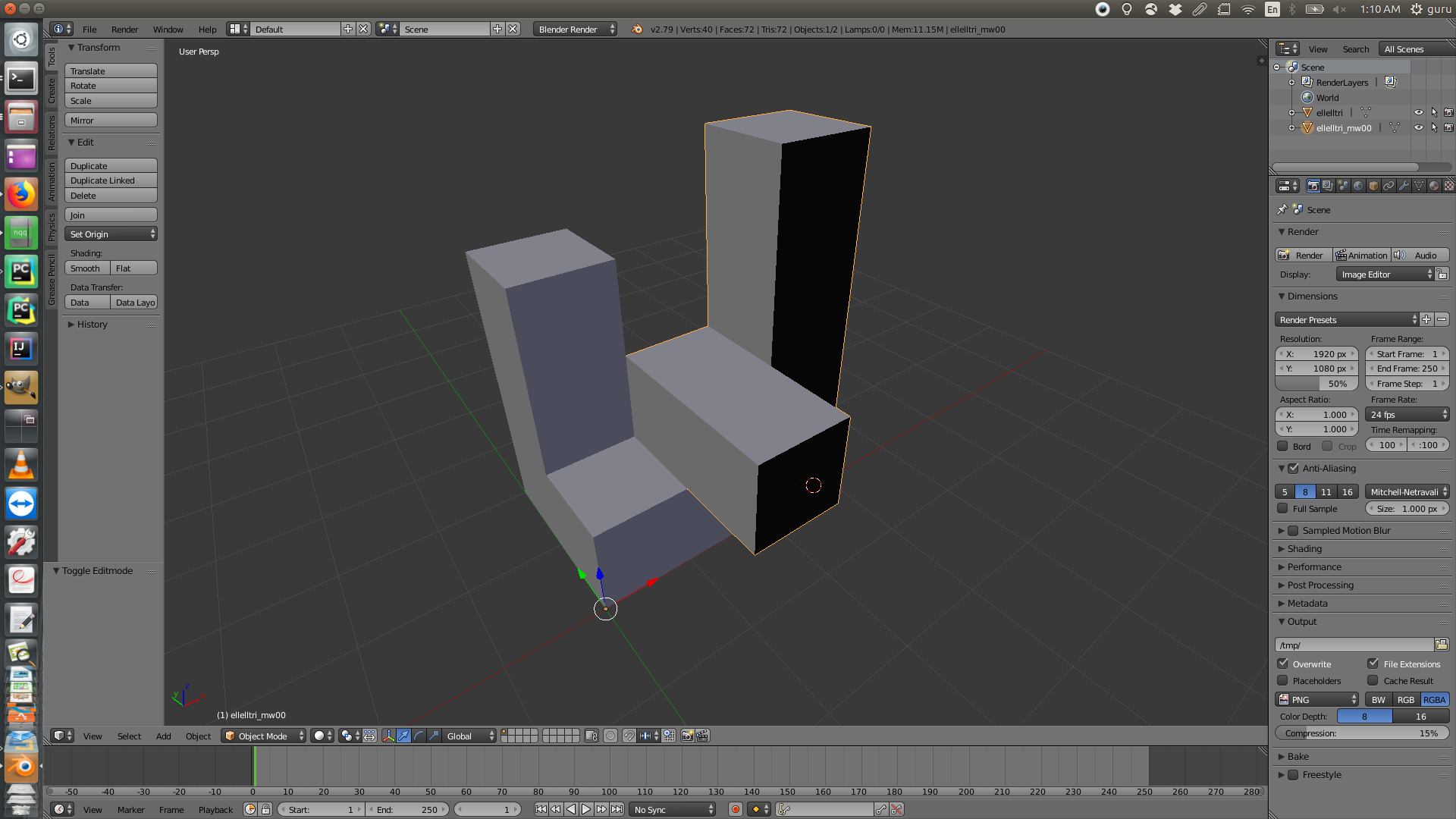
Here are some examples of .obj objects before and after applying the transformations. If you are interested, you could find more examples here or download directly from the the download links on this page. You will find 'driver' files in driver folder that describe what transformation to apply on which object file (from models folder). The corresponding outputs are stored in the driver_outputs in a folder named after the driver files.
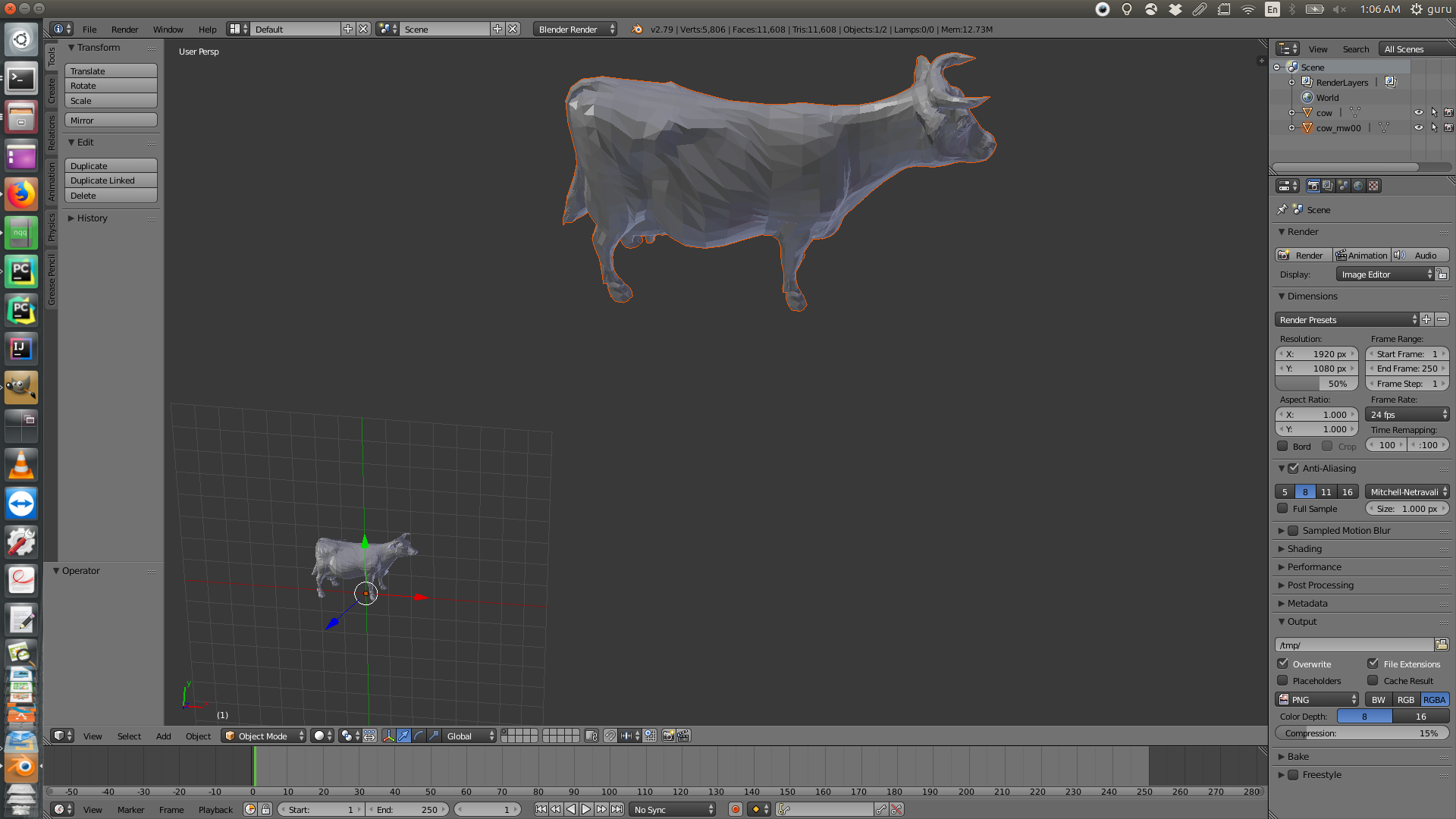
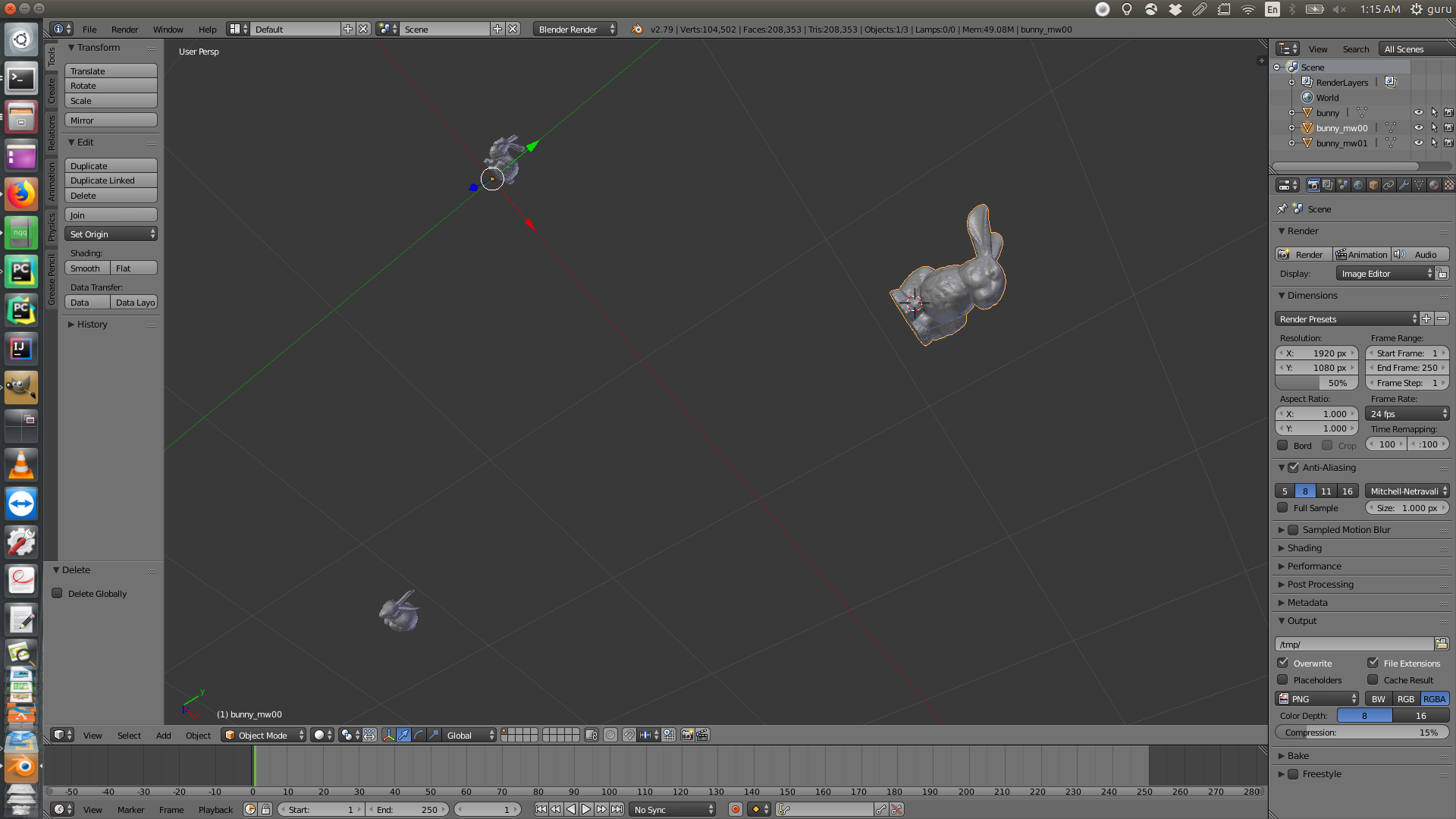
Note: Some of the content for this post is taken from course material of CS410 (CSU) written by Prof. Ross Beveridge.